Optimized Wordle words
If you're anything like me, lately you have found yourself trying to cook up strategic five letter words to feed into Wordle, a daily word game that has become popular enough recently that the New York Times succumbed to the temptation to acquire it. In this post we'll derive a set of five words optimized to increase your chances of winning.
How to Play Wordle
Your goal in Wordle is to determine a secret five letter word. You're given six chances to guess the word, and each guess yields clues about the secret word. For example, suppose you guess the world UNLIT and are presented with the following:

Wordle is telling you that:
- The letters U, N, and I are not in the secret word.
- The letter L is in the secret word, but not in the third position.
- The letter T is in the secret word, and in the fifth position.
As you guess more words, you'll get more clues, eventually allowing you to make a precise guess about the secret word and win the game. Hopefully!
The Strategy
Let's play a little bit of Wordle and see if we can suss out a strategy. We'll open up Wordle and guess our first word, ZAPPY:

Great, we've already got some clues! We know A is in the secret word, and we know it's not in the second position. We also know Z, P, and Y are not in the secret word.
There's a couple problems with our first word guess, though. First, Z is a rarely used letter in the english language. We'd be better off guessing letters that are most commonly used (assuming the secret words aren't biased!). Second, there's two Ps in ZAPPY. We don't learn anything from that second P, so we wasted a whole letter slot. We could know two letters right now instead of one!
Let's guess another word and see what else we can learn. Let's try PANTS:

Excellent, more clues - we now know that T is in the secret word, and not in the fourth position. We also learned that S and N are not in the secret word.
Again, though, there's a couple problems with our second word guess. First, we already know P isn't in our word, why are we guessing it again?! That was silly. We also already know A is in our word, so should we bother with it again? Perhaps, if we were desperate to know the correct position of the letter A, we could use it in our guess in a new position. But here, we've wasted that opportunity by placing it in an already known bad position!
Let's review what we've learned about our strategy. We should:
- Prefer guessing letters that are more commonly used, like S, and avoid rarely used ones, like Z.
- Avoid reusing letters.
- If we do reuse letters, prefer letters that we know are in our word, and try to place them in previously untested positions.
Following this strategy, we should be able to come up with words that give us more information about which letters are in the secret word, and where they are. One more thing though - what is more important, knowing which letters are in the word, or knowing what position they are in?
Let's take a look at two circumstances. Let's suppose we know either:
- Our secret word is composed of the letters T, F, A, O, and L, but we know nothing about the position of those letters, or...
- Our secret word has the letter T in the last position, but we don't know any other letters.
A quick scan of the Wordle word list reveals three words composed of the letters T, F, A, O, and L: FLOAT, ALOFT, and FLOTA, but there are 727 words that end in T! So let's add one more rule to our strategy:
- Prefer learning more letters to learning letter position.
The Wordle dictionary
Now that we have a strategy, let's see what we can do about implementing it. First, we want to guess words with letters that are commonly used. In order to figure out which letters those are, we'll generate a histogram of how frequently each letter occurs in English words. To do that, we'll need a list of words. We don't want to use any old word list, though, we want to use the list of words Wordle uses. To do that, load up the Wordle website, open your developer console (often F12), and prettify the code. Then scroll through, looking for word lists. Ah, here we go:
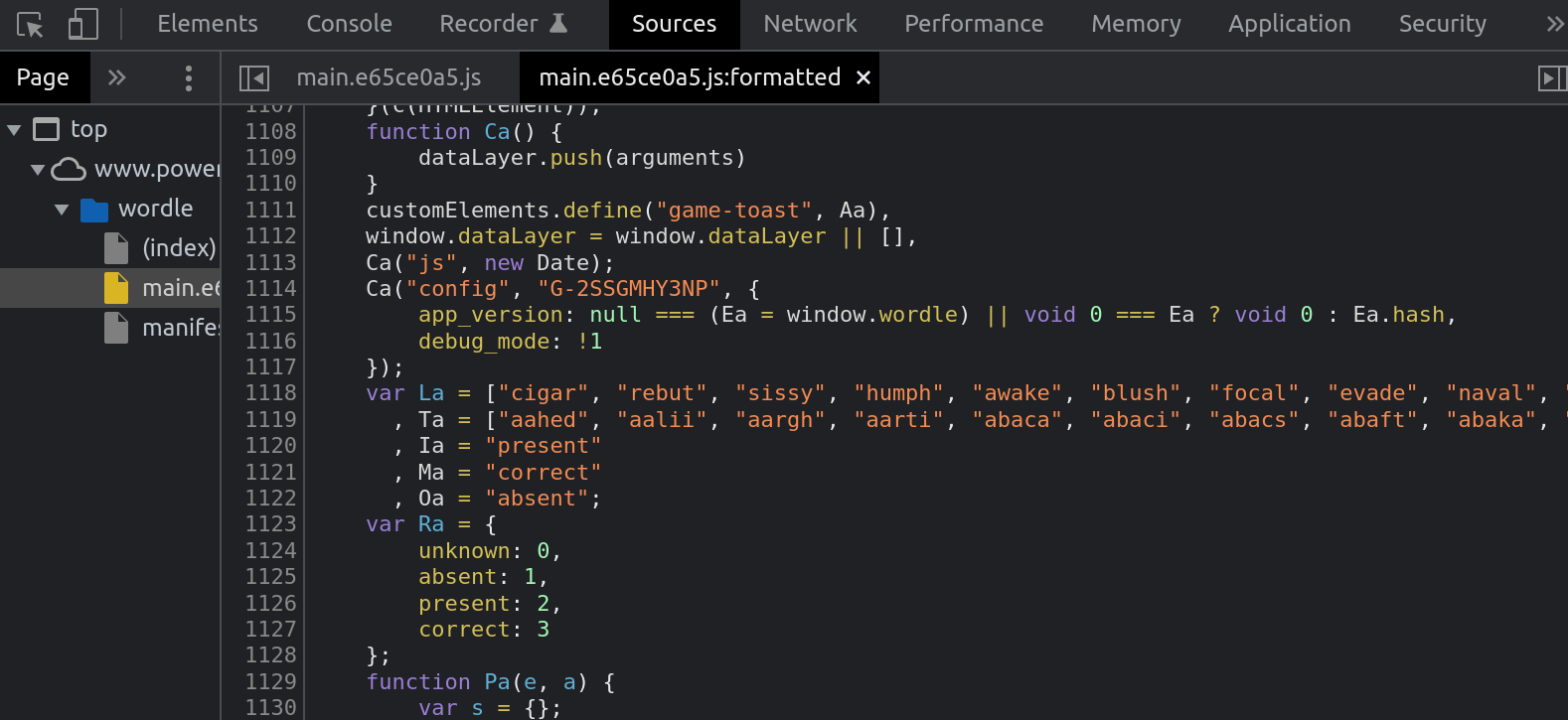
See lines 1118 and 1119, that look like this?
var La = ["cigar", "rebut", "sissy", ...
, Ta = ["aahed", "aalii", "aargh", ...Those two arrays contain our word list. There's two, though - why is that? It turns out the first list is the list of secret words (in order, so be careful about looking too close if you don't want any spoilers!), and the second list is the remaining words in the word list. The lists are mutually exclusive - there are no words from the first list in the second, and vice versa. So the total word list is the combination of both arrays of words. If you're curious, there's 2,315 words in the secret word list (6.34 years worth!) and 10,657 words in the remaining word list, for a total of 12,972 words.
While we could build our histogram from the smaller secret word list, that feels a bit like cheating - we're not supposed to know what those words are! So we'll build it out of the total 13K word list.
In code, here's what building that histogram might look like:
const histogram: Record<string, number> = {};
for (const word of words) {
for (const letter of word) {
if (histogram[letter] === undefined) {
histogram[letter] = 0;
}
histogram[letter]++;
}
}And here's the result:

Generating Word Lists
Now that we know the frequency of each letter in the Wordle word list, we can calculate a score for each word and sort the results. We'll iterate through each letter of each word and increment the score for that word by the frequency of that letter. As we iterate through each letter, we'll skip duplicates so that we don't over-reward words with repeated letters (like ZAPPY!).
const wordScores: Record<string, number> = {};
for (const word of words) {
const unique = new Set(word); // Using Set removes duplicates.
wordScores[word] = 0;
for (const letter of unique) {
wordScores[word] += histogram[letter];
}
}
const sortedWordScores = Object.entries(wordScores).sort((a, b) => b[1] - a[1]);So we've scored our words and sorted them by score, so now all we need to do is take the top five words from that list and we're done, right? Let's take a look!
| Word | Score |
|---|---|
| Arose | 27913 |
| Aeros | 27913 |
| Soare | 27913 |
| Arise | 27234 |
| Raise | 27234 |
| Aesir | 27234 |
| Reais | 27234 |
| Serai | 27234 |
| Aloes | 27126 |
| Stoae | 27050 |
Oh, whoops. It looks like there's some degenerate scores in there - some words have the same scores. Also, the top three words have all the same letters, so just grabbing the top five words would violate our strategy to avoid repeating letters.
This is starting to look like a tree traversal problem. Instead of picking the top five words, let's do this:
- Make a list of the top-scoring words (in the example above, AROSE, AEROS, and SOARE).
- For each word, set the value of the letter frequencies to zero so that we don't reward repeated letters in later words.
- Repeat steps one and two above until we have a set of five word lists, keeping track of the total score of each word list the whole way.
We'll write a recursive function to accomplish this:
interface ScoredWordList {
words: string[];
score: number;
}
function getScoredWordLists(
letterFrequencies: Record<string, number>,
previousWords: string[],
previousScore: number
): ScoredWordList[] {
// Make a copy of the letter frequencies.
letterFrequencies = JSON.parse(JSON.stringify(letterFrequencies));
// Zero out letters we've already used.
for (const word of previousWords) {
for (const letter of word) {
letterFrequencies[letter] = 0;
}
}
// Score every word in the total Wordle word list.
const wordScores: Record<string, number> = {};
for (const word of words) {
const unique = new Set(word);
wordScores[word] = 0;
for (const letter of unique) {
wordScores[word] += letterFrequencies[letter];
}
}
// Sort them by score.
const sortedWordScores = Object.entries(wordScores).sort((a, b) => b[1] - a[1]);
// Find the best score and keep only the words that have that score.
const bestScore = sortedWordScores[0][1];
const bestWords: string[] = [];
for (const ws of sortedWordScores) {
if (ws[1] !== bestScore) {
break;
}
bestWords.push(ws[0]);
}
// If this is the last word, return the word list and score.
if (previousWords.length === 4) {
return bestWords.map((w) => ({
words: previousWords.concat(w),
score: bestScore + previousScore,
}));
}
// Otherwise, recurse deeper into the tree and add more words.
return bestWords
.map((w) =>
getScoredWordLists(letterFrequencies, previousWords.concat([w]), bestScore + previousScore)
)
.flat();
}Now let's invoke our recursive function, sort the results, and take a look:
const scoredWordLists = getScoredWordLists(histogram, [], 0);
const sortedScoredWordLists = scoredWordLists.sort((a, b) => b.score - a.score);| Word list | Total Score |
|---|---|
| Arose, unlit, dumpy, whack, befog | 63041 |
| Arose, unlit, dumpy, chawk, befog | 63041 |
| Arose, unlit, dumpy, chowk, befog | 63041 |
| Arose, unlit, dampy, whack, befog | 63041 |
| Arose, unlit, dampy, chawk, befog | 63041 |
| Arose, unlit, dampy, chowk, befog | 63041 |
| Arose, until, dumpy, whack, befog | 63041 |
| Arose, until, dumpy, chawk, befog | 63041 |
| Arose, until, dumpy, chowk, befog | 63041 |
| Arose, until, dampy, whack, befog | 63041 |
| Arose, until, dampy, chawk, befog | 63041 |
| Arose, until, dampy, chowk, befog | 63041 |
| Aeros, unlit, dumpy, whack, befog | 63041 |
| Aeros, unlit, dumpy, chawk, befog | 63041 |
| Aeros, unlit, dumpy, chowk, befog | 63041 |
| Aeros, unlit, dampy, whack, befog | 63041 |
| Aeros, unlit, dampy, chawk, befog | 63041 |
| Aeros, unlit, dampy, chowk, befog | 63041 |
| Aeros, until, dumpy, whack, befog | 63041 |
| Aeros, until, dumpy, chawk, befog | 63041 |
| Aeros, until, dumpy, chowk, befog | 63041 |
| Aeros, until, dampy, whack, befog | 63041 |
| Aeros, until, dampy, chawk, befog | 63041 |
| Aeros, until, dampy, chowk, befog | 63041 |
| Soare, unlit, dumpy, whack, befog | 63041 |
| Soare, unlit, dumpy, chawk, befog | 63041 |
| Soare, unlit, dumpy, chowk, befog | 63041 |
| Soare, unlit, dampy, whack, befog | 63041 |
| Soare, unlit, dampy, chawk, befog | 63041 |
| Soare, unlit, dampy, chowk, befog | 63041 |
| Soare, until, dumpy, whack, befog | 63041 |
| Soare, until, dumpy, chawk, befog | 63041 |
| Soare, until, dumpy, chowk, befog | 63041 |
| Soare, until, dampy, whack, befog | 63041 |
| Soare, until, dampy, chawk, befog | 63041 |
| Soare, until, dampy, chowk, befog | 63041 |
Interesting - all the word list scores are the same! If we alphabetize each word and remove duplicate letters we're left with the following for every word list: AEORS, ILNTU, DMPY, CHKW, and BFG. So if we consider these results with only letter score in mind, the identical scores make sense. We could have skipped keeping track of the total score, but we couldn't have known that beforehand, so it's good that we checked!
Positionally Scored Word Lists
We've taken into account the letter scores, but we haven't accounted for positional clues. To do that we'll assign a score to each word list according to how much positional data it affords us. We'll loop over each word in the list and keep track of the letters used at each position. Each time we see a new letter at a position, we'll increment the score for that word list:
// Filter out any word lists that score worse than the best. (There are none,
// but you need to know where bestScoredWordLists comes from!)
const bestScoredWordLists = scoredWordLists.filter(
(wl) => wl.score === sortedScoredWordLists[0].score
);
const positionallyScoredWordLists: ScoredWordList[] = [];
for (const wl of bestScoredWordLists) {
const positions: string[][] = [[], [], [], [], []];
let score = 0;
for (const word of wl.words) {
for (let i = 0; i < 5; i++) {
if (positions[i].includes(word[i])) {
continue;
}
score++;
positions[i].push(word[i]);
}
}
positionallyScoredWordLists.push({ words: wl.words, score });
}Now let's sort the results and see what we've got:
positionallyScoredWordLists
.sort((a, b) => b.score - a.score)
.forEach((swl) => console.log(...swl.words, swl.score));| Word list | Positional Score |
|---|---|
| Arose, unlit, dumpy, whack, befog | 25 |
| Arose, unlit, dumpy, chawk, befog | 25 |
| Arose, unlit, dampy, whack, befog | 25 |
| Arose, unlit, dampy, chawk, befog | 25 |
| Arose, until, dumpy, whack, befog | 25 |
| Arose, until, dumpy, chawk, befog | 25 |
| Arose, until, dampy, whack, befog | 25 |
| Arose, until, dampy, chawk, befog | 25 |
| Soare, unlit, dumpy, chowk, befog | 25 |
| Soare, unlit, dampy, chowk, befog | 25 |
| Soare, until, dumpy, chowk, befog | 25 |
| Soare, until, dampy, chowk, befog | 25 |
| Arose, unlit, dumpy, chowk, befog | 24 |
| Arose, unlit, dampy, chowk, befog | 24 |
| Arose, until, dumpy, chowk, befog | 24 |
| Arose, until, dampy, chowk, befog | 24 |
| Soare, unlit, dumpy, whack, befog | 24 |
| Soare, unlit, dumpy, chawk, befog | 24 |
| Soare, unlit, dampy, whack, befog | 24 |
| Soare, unlit, dampy, chawk, befog | 24 |
| Soare, until, dumpy, whack, befog | 24 |
| Soare, until, dumpy, chawk, befog | 24 |
| Soare, until, dampy, whack, befog | 24 |
| Soare, until, dampy, chawk, befog | 24 |
| Aeros, unlit, dumpy, whack, befog | 23 |
| Aeros, unlit, dumpy, chawk, befog | 23 |
| Aeros, unlit, dumpy, chowk, befog | 23 |
| Aeros, unlit, dampy, whack, befog | 23 |
| Aeros, unlit, dampy, chawk, befog | 23 |
| Aeros, unlit, dampy, chowk, befog | 23 |
| Aeros, until, dumpy, whack, befog | 23 |
| Aeros, until, dumpy, chawk, befog | 23 |
| Aeros, until, dumpy, chowk, befog | 23 |
| Aeros, until, dampy, whack, befog | 23 |
| Aeros, until, dampy, chawk, befog | 23 |
| Aeros, until, dampy, chowk, befog | 23 |
There's still a lot of degenerate solutions, but we have narrowed things down a bit more. Let's compare the top and bottom entries of that list. We'll arrange them vertically so that we can more easily pick out positional repeats:
| Score 25 | Score 23 |
|---|---|
| AROSE | AEROS |
| UNLIT | UNTIL |
| DUMPY | DAMPY |
| WHACK | CHOWK |
| BEFOG | BEFOG |
While there are no positional repeats in the first list, the positions of the letters E and O are repeated in AEROS and BEFOG in the second.
Final Solution
The top twelve solutions are degenerate - per our strategy, they will all yield the same results. Some of those words are a little bit more weird than others, though, so I'm going to make an opinionated choice and select the following as the best, least weird set of words for our final solution:
Now, let's give it a shot! We'll open up today's Wordle and plug in our words, starting with AROSE:

Aha, we got two letters, and lucky us, we know where they are. Let's continue with UNTIL:

Great, we got two more letters! This is probably enough to guess the word, but let's keep going with DUMPY:

No luck! Next, WHACK:

Nope! Maybe BEFOG?

Aha, F! We have all our letters now, A, O, T, L, and F. As mentioned earlier, there's three words with those letters: FLOAT, ALOFT, and FLOTA. Only one of those has an A and an O in the first and second positions, respectively, though. Let's try it:

Nailed it!
Thanks for reading this far. Hit me up on twitter if you've come up with your own optimized set of words, I'd like to try them out!